Mercator 投影
2021-09-19 12:00:00
作为一个轻度的地图控,我一直想探索地图投影这一块的知识。不知道大家有没有这样的疑问:高德地图、谷歌地图为什么都采用 Mercator 投影?
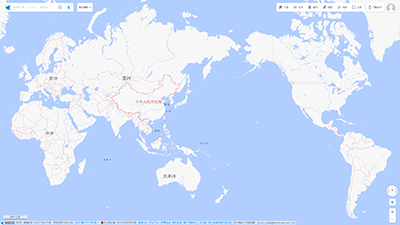
这种地图高纬度地区严重失真,格陵兰岛看起来比非州还要大,究竟有什么好处?

等距柱状投影
因为本文涉及的投影方式都是圆柱投影,所以在介绍 Mercator 投影之前,不妨先了解一下比较简单的等距柱状投影。
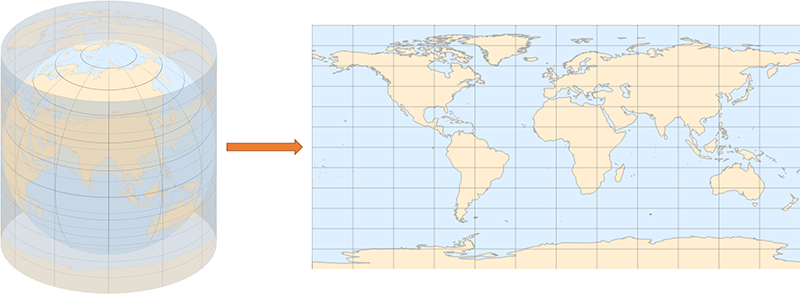
这种投影用一个底面直径、高均等于地球直径的圆柱面卡住地球,圆柱的轴线与地轴重合。从地轴上一点出发,沿与赤道平行的方向把地表上一点投影到圆柱面上,再把圆柱面展开,就得到了等距柱状投影的地图。投影形成的各矩形网格单元具有相同的长宽。我愿用一句话来形容这个过程:

所谓地图投影,无非就是把地表一点 我瞎猜的)?等距柱状投影的映射关系足够简单:
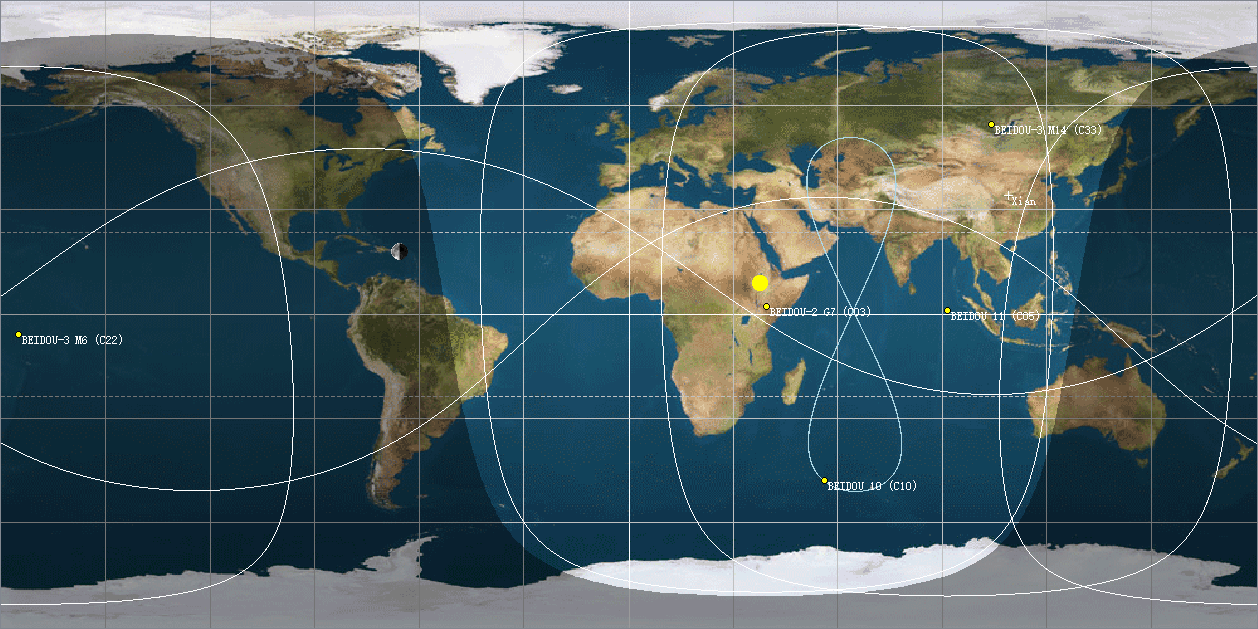
由于映射关系简单,所以在轨道力学中,经常用等距柱状投影绘制航天器的星下点轨迹,因为基本不需要经过复杂的转换。下面是几颗航天器的星下点轨迹:
Mercator 投影
首先需要交代 Mercator 投影的提出年代是 16 世纪,彼时大航海时代方兴未艾,世界需要一张准确清晰的航海图。对于远洋航行来说,最方便的地图是能够让航线在地图上是一条直线,这样只需用直线把起点与目的地连接起来,就得到了航线。
1569 年,Gerhardus Mercator 出版了他的世界地图,在这张地图上,平行的经线与平行的纬线垂直交错形成了经纬网,并且投影前后角度没有发生变化。这是一个开拓性的创造,Mercator 开创了地理学史新的篇章。

(Gerhardus Mercator 1512-1594)
和等距柱状投影一样,Mercator 投影也是圆柱投影,投影遵循等角约束(具体如何实现,先按下不表)
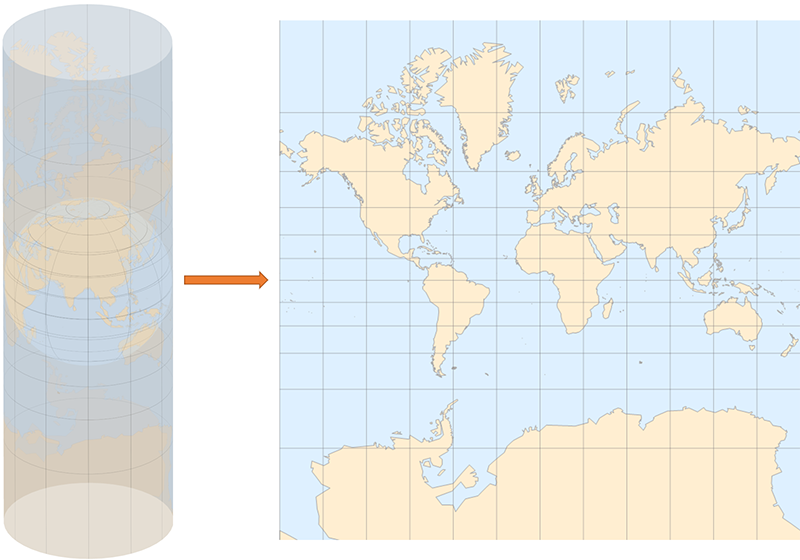
地图上经纬线垂直的意义不言而喻,需要说明一下投影前后角度不变的意义:
在 Mercator 的年代,航海导航全靠指南针,指南针会给出当地经线的方向,船的航行方向与经线夹成一定的角度。在 Mercator 的地图上,由于经线互相平行,我们任意画一条直线航线,会发现它与每条经线所夹的角度是相同的,那么根据角度不变,还原回地表,这条航线与球面的每条经线所夹的角度依然是相同的,这样我们让船的航行方向与指南针始终夹成这个角度,就可以实现沿着这条航线航行,到达目的地。这样的航线被称为等角航线。
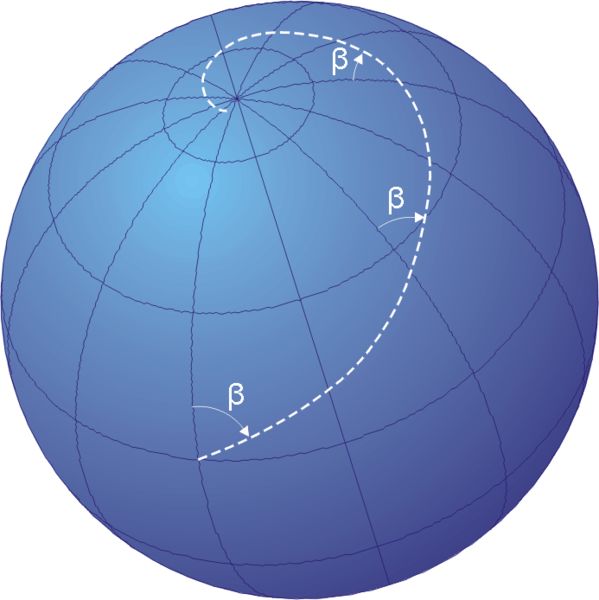
在 Mercator 的地图上,用直线就可以轻松规划出一条等角航线,排除风浪等因素的干扰,只要利用指南针使得航行方向保持这个角度,就可以导航到目的地,非常便于测量和纠正,这就是 Mercator 的地图的先进性,直到今天仍然没有过时。
回到本文开头的问题,各大地图软件为什么偏爱 Mercator 投影,答案就是方向不变。垂直的十字路口在 Mercator 投影上依然是垂直的,笔直的道路在 Mercator 投影上依然是笔直的。用一张图来说明:
下面,我们将根据等角约束,分别考虑地球是球体和椭球体两种情况,推导出 Mercator 投影的投影公式。
球体
在平面投影图上,分别以
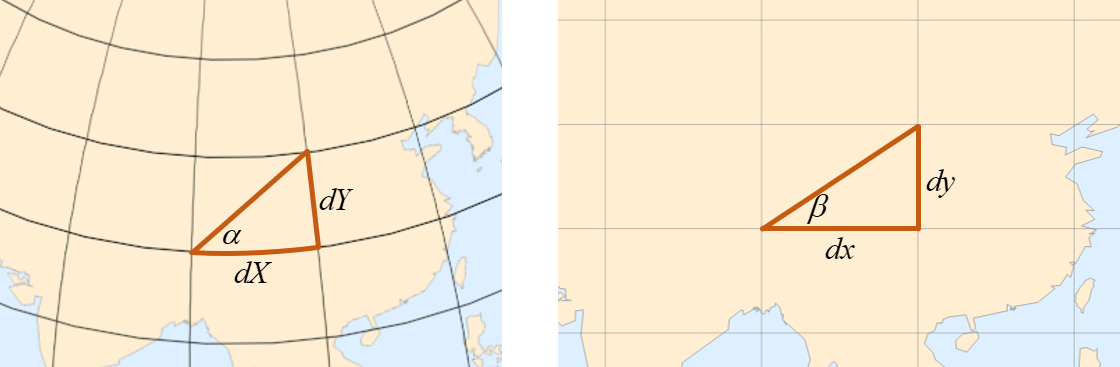
有
引入等角约束,即必须满足:
另外
所以
把上式代入到等角约束的表达式中,化简,得到
两边积分,得到
另外,根据所建直角坐标系的特点
又由于纬度
还有一些变形形式:
Mercator 投影的逆变换:
当
即 Web Mercator 投影表示的是
椭球体
设椭球的扁率为
引入椭球条件下的等角约束:
所以
两边积分,得到
椭球条件下,Mercator 投影的投影公式为:
横轴 Mercator 投影
横轴 Mercator 投影是在 Mercator 投影的基础上,把投影圆柱倾斜
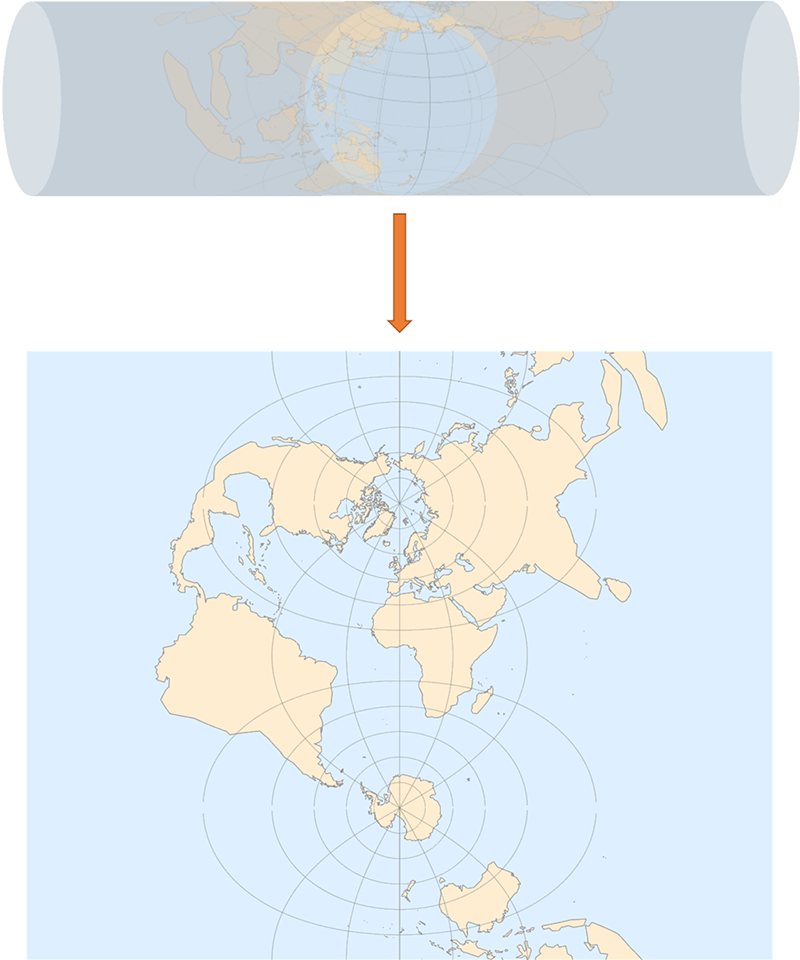
和 Mercator 投影相反,它的特点是两级的变形最小,赤道的变形最大。
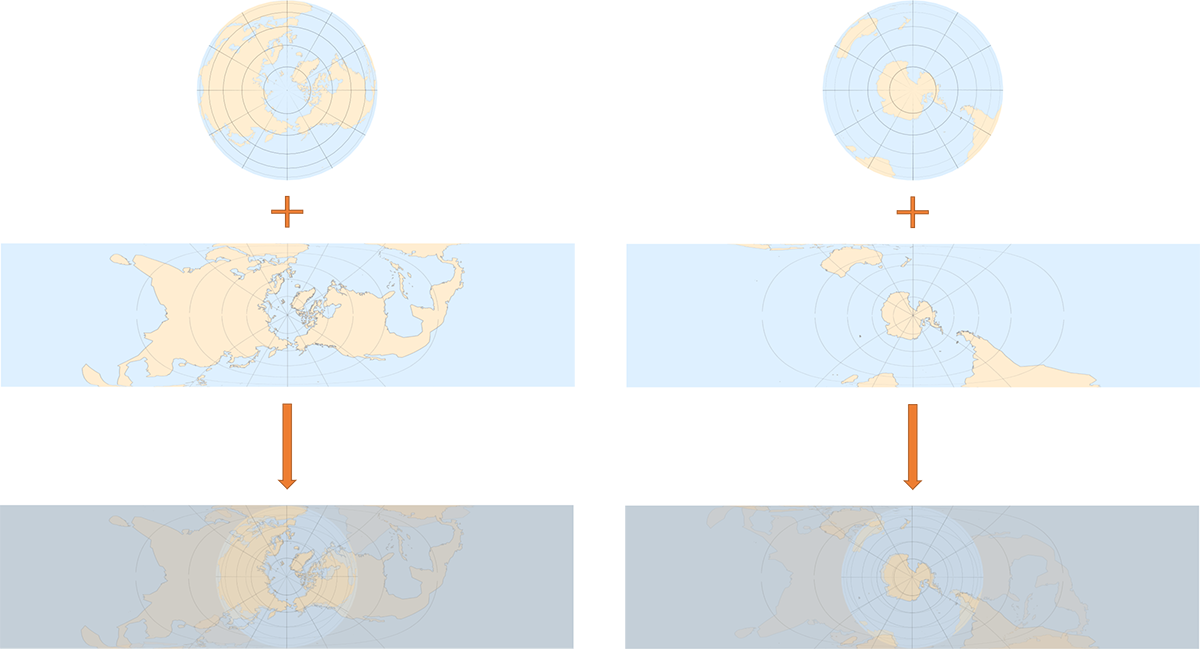
它的投影公式为:
具体推导过程暂且不表,后文的斜轴 Mercator 投影部分会进行推导。

看到横轴 Mercator 投影的地图,不由得让我想起初中地理课本上解释地球仪的一张插图,书上的插图我已经找不到了,这里大概复现了一下:
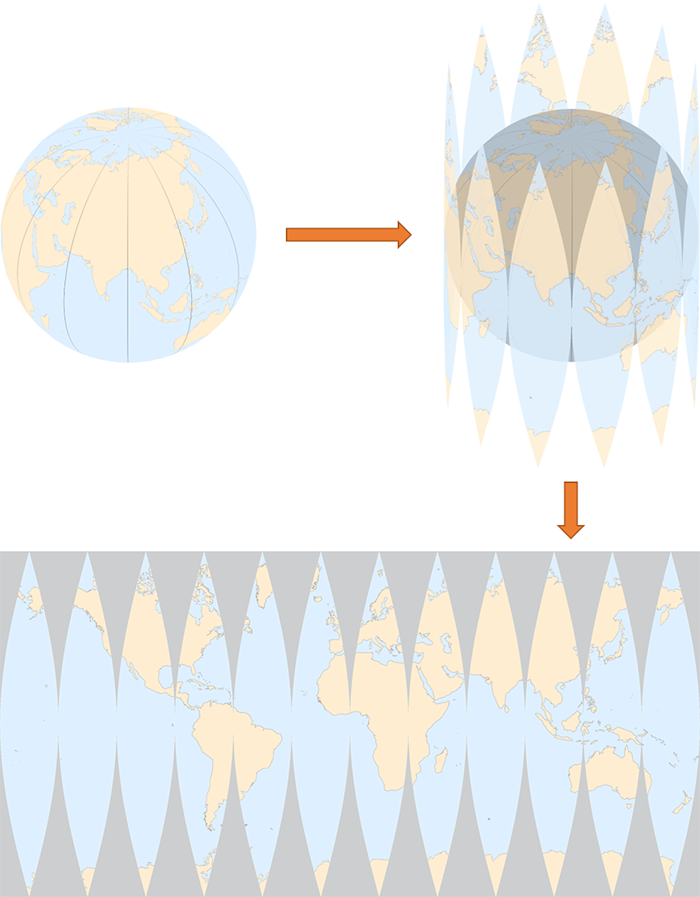
大概意思就是:像剥桔子皮一样,把地表沿着一些经线剥开,再展成平面图。它的逆过程就是制作地球仪的过程。上图中的每一个梭形区域都是用横轴 Mercator 投影计算出来的。
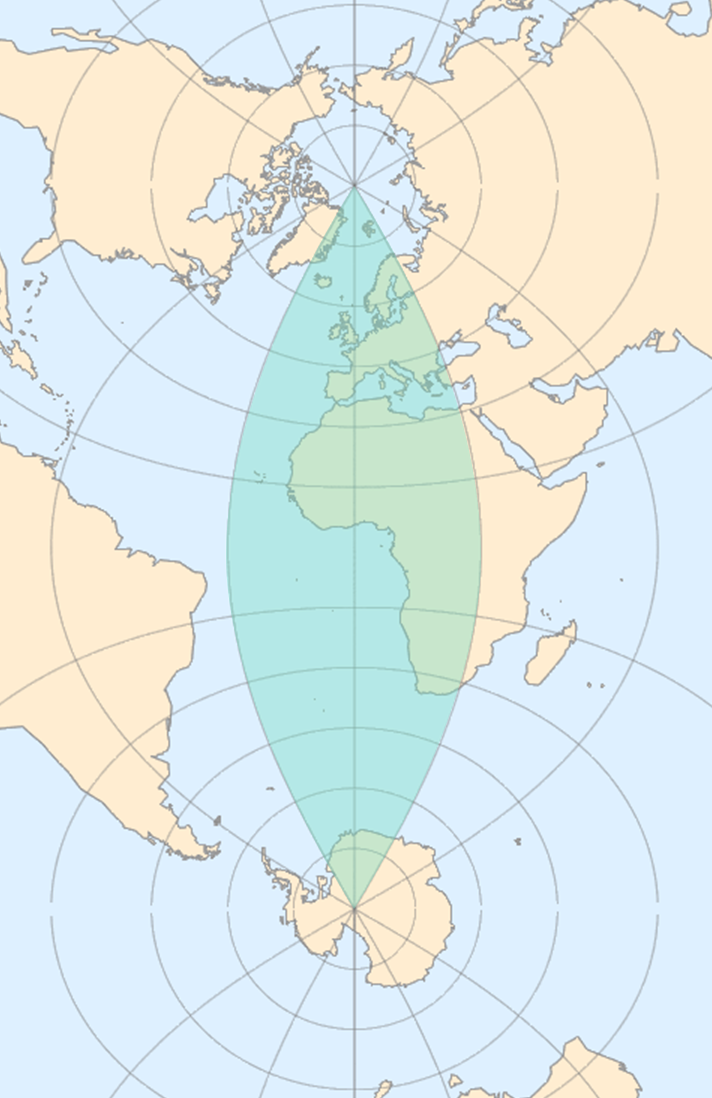
三种投影的对比
以上介绍了等距柱状投影、Mercator 投影、横轴 Mercator 投影,下面分别从投影前后角度的变化和面积的变化进行对比。
角度的变化
前面已经介绍了等角航线,这种航线在导航方面容易实现,但是它的航程如何呢?很可惜,等角航线的航程不是最短的,两点间最短的航线是大圆航线。
通过地面上任意两点和地心做一平面,平面与地球表面相交得到的圆周是大圆,两点之间的大圆劣弧线就是大圆航线。
但是大圆航线与各经线的夹角不是恒定的,沿大圆航线航行需要不断地调整方向。
在地球表面取 4 个地点,分别构造 3 条大圆航线(红色)和 3 条等角航线(紫色),如下图(这里不纠结航线经过陆地的问题,或者把它们理解为飞机的航线)
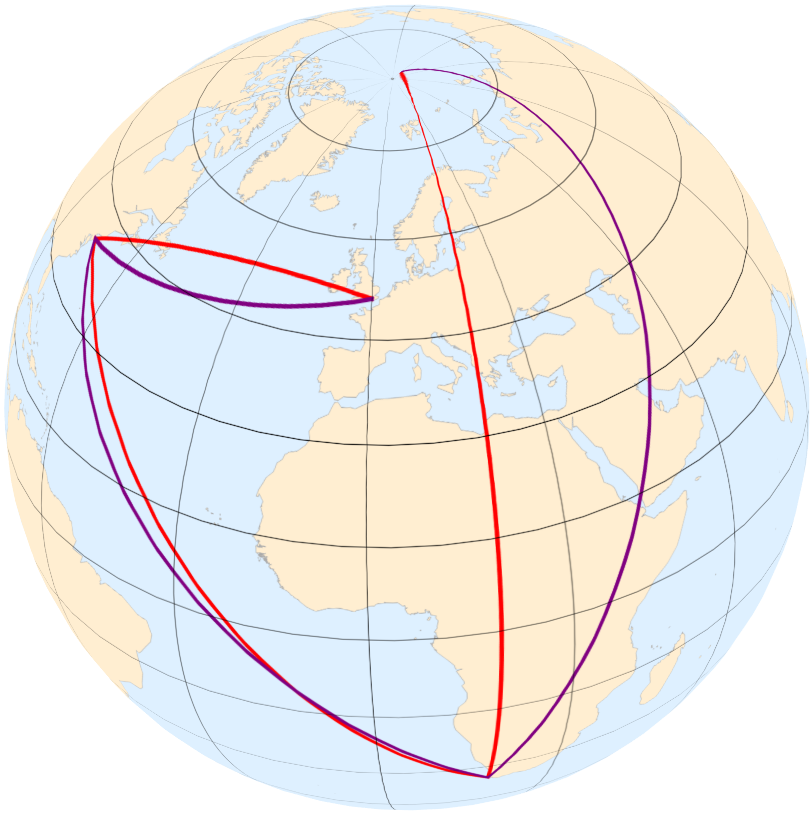
等距柱状投影
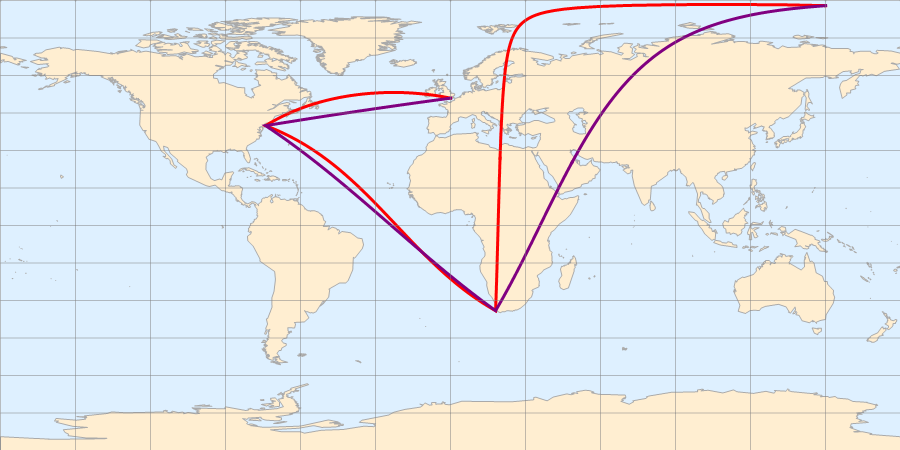
Mercator 投影
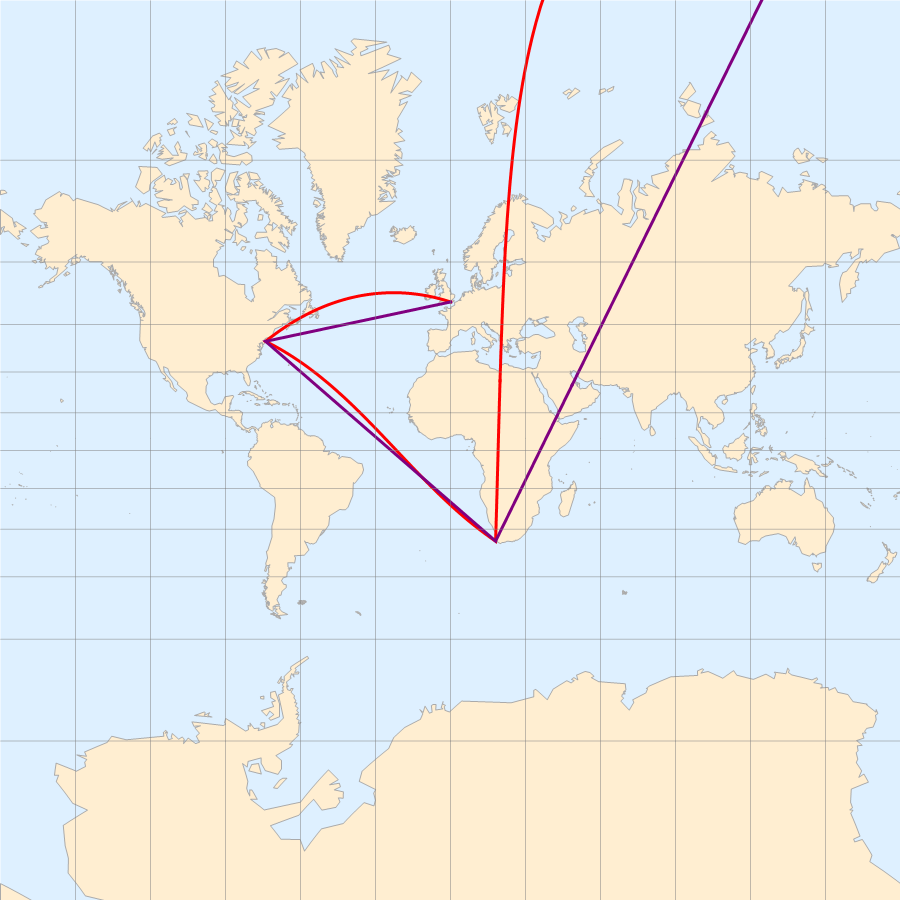
横轴 Mercator 投影
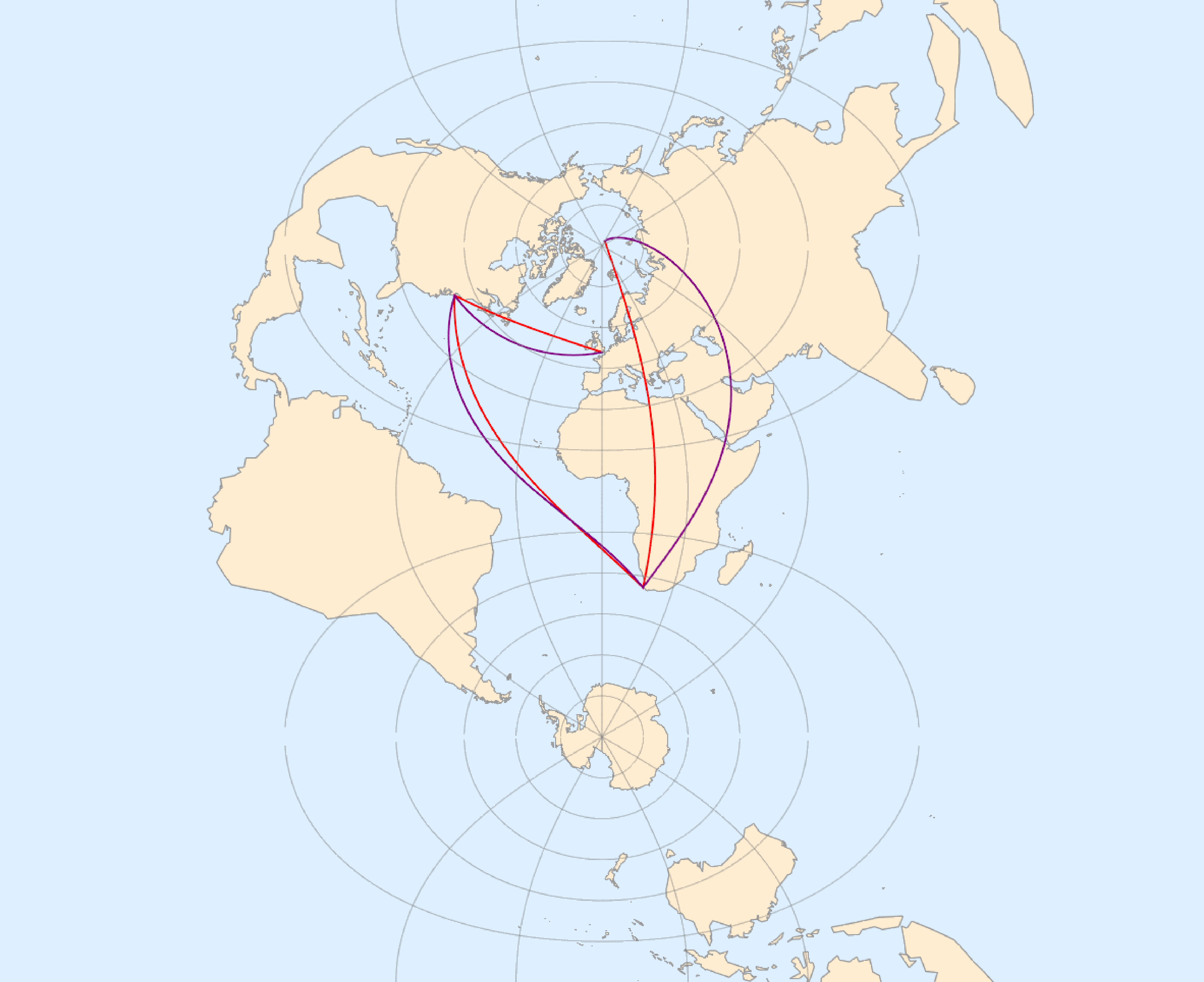
通过对比可以发现:
- 在 Mercator 投影里,等角航线的确是直线,而大圆航线不是。
- 在某些情况下,大圆航线和等角航线比较接近。此时完全可以沿着等角航线航行。在某些情况下,大圆航线和等角航线相差非常明显。
面积的变化
提示:以下内容可能引起密集恐惧症患者不适,请有选择地阅读!
在地球表面取若干等面积的圆形区域,如下图:
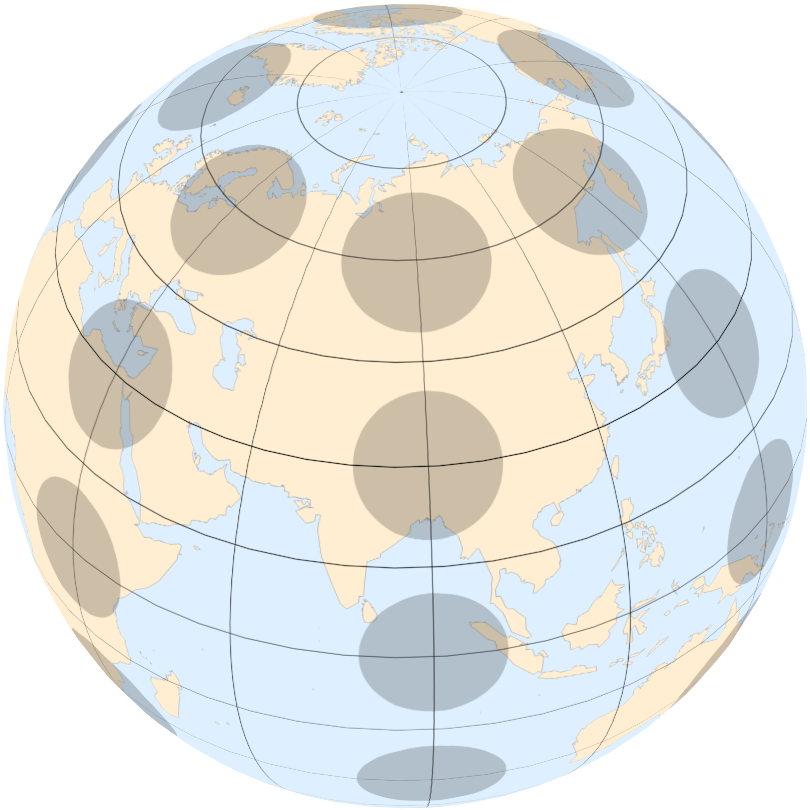
等距柱状投影
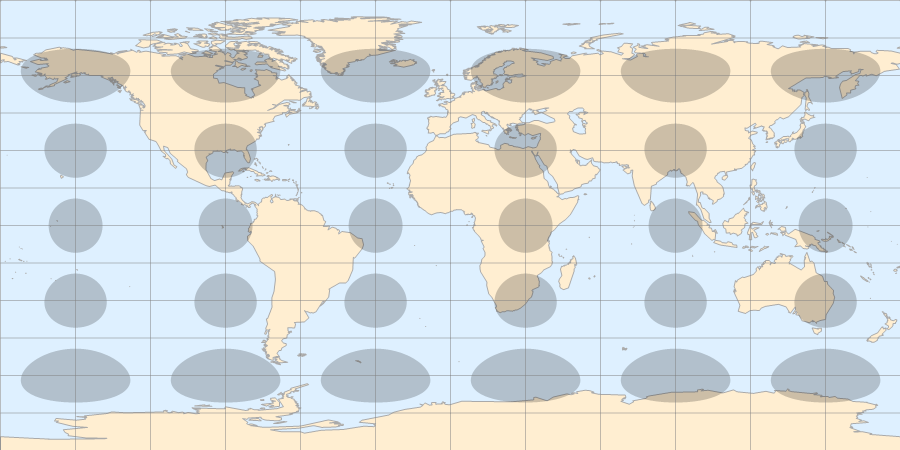
Mercator 投影
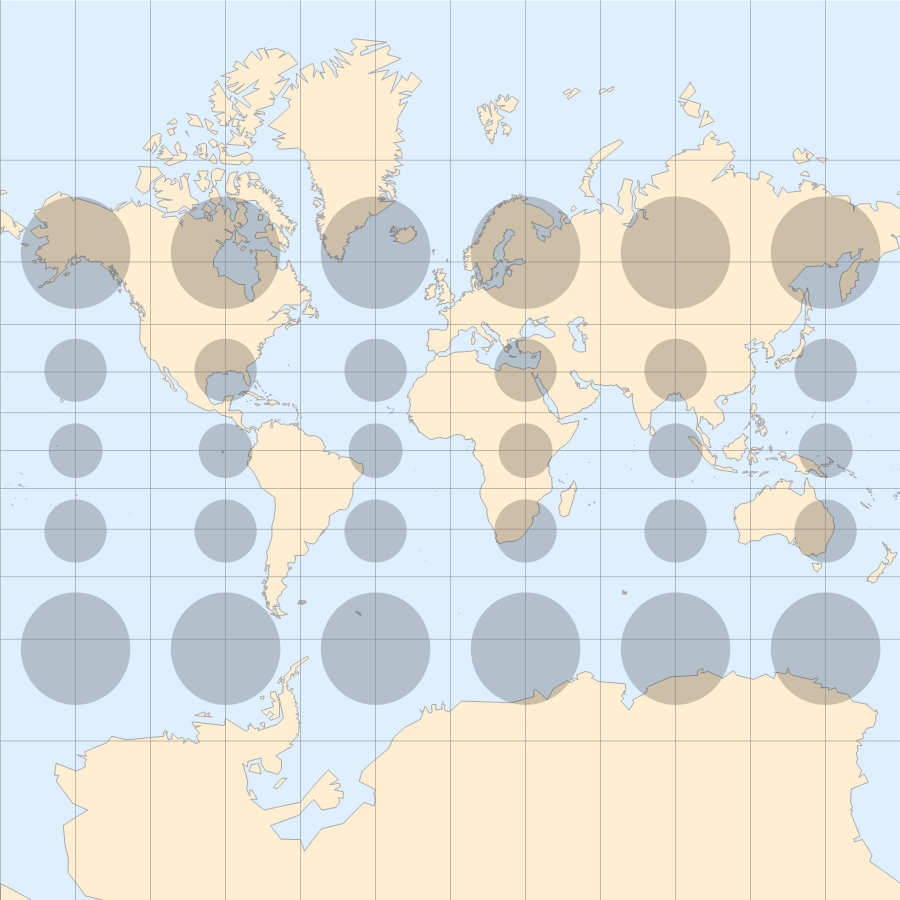
横轴 Mercator 投影
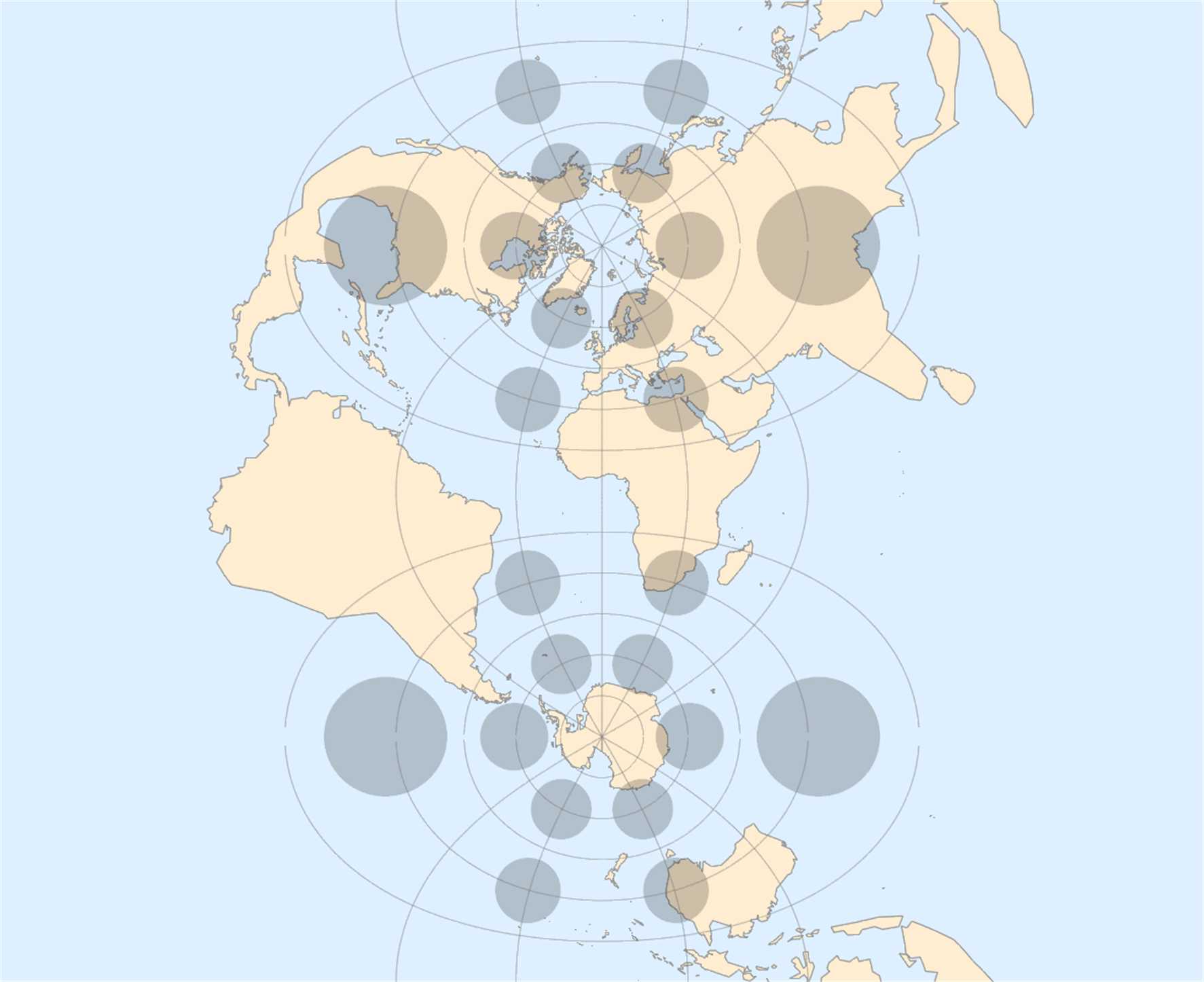
通过对比可以发现:
- 三种投影都改变了圆形区域的面积。
- Mercator 投影越靠近两级,面积被放大地越多;横轴 Mercator 投影越靠近赤道,面积被放大地越多。
- 对于 Mercator 投影和横轴 Mercator 投影,投影前后形状没发生变化,再次体现了角度不变性。
斜轴 Mercator 投影
在横轴 Mercator 投影中,把投影圆柱倾斜了
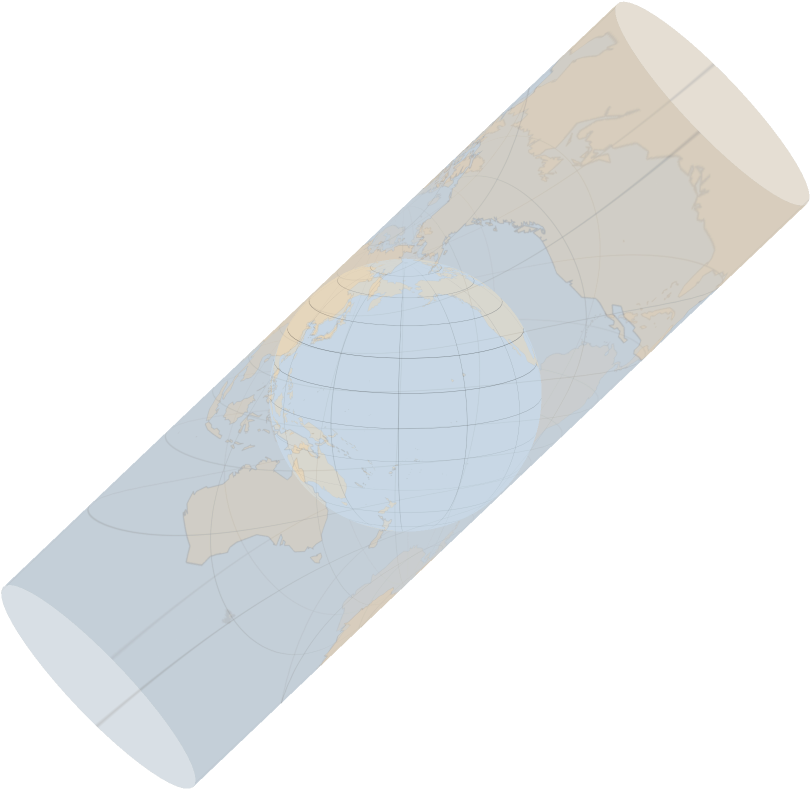
这样形成的投影图称为斜轴 Mercator 投影,先预览一下倾斜
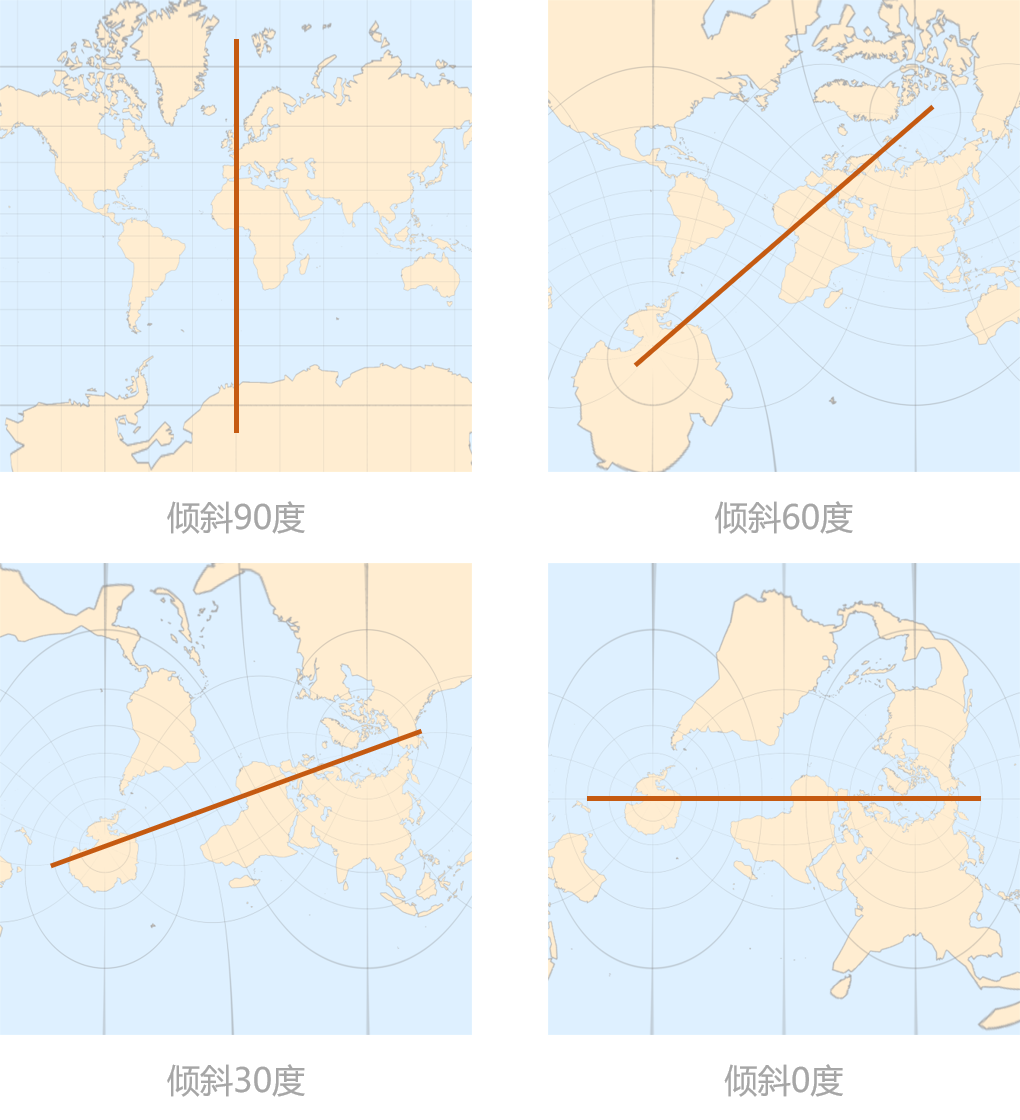
斜轴 Mercator 投影的投影公式为:
下面进行推导:
记
示意图如下:
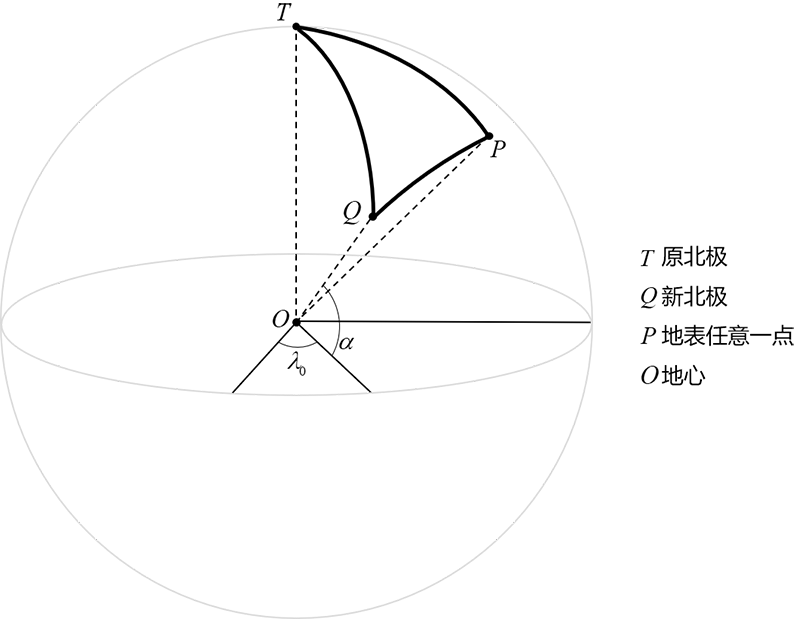
定义
角度的几何关系罗列如下:
根据球面三角的公式,有:
和
根据这两个公式,可以导出
这样就得到了
在北极
整理前面得到的各转换关系,得到
当
此时,把
得证。
斜轴 Mercator 投影的逆变换为
下面是本文最燃的一部分,让我们把倾斜角
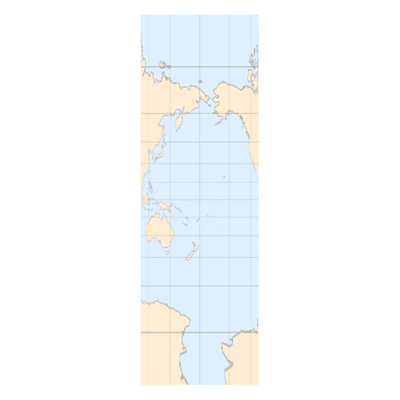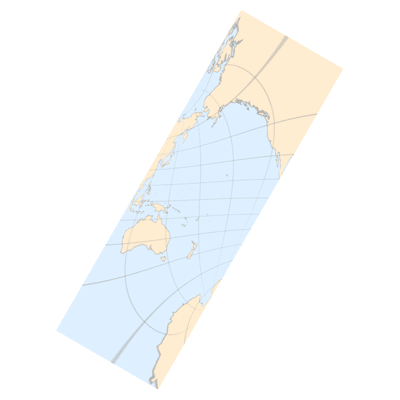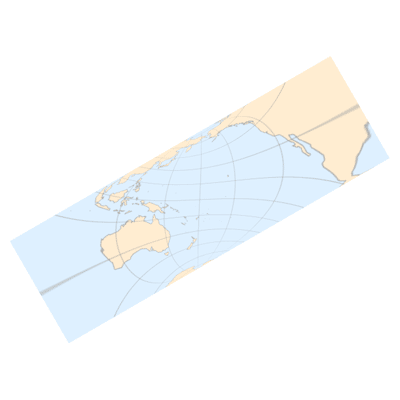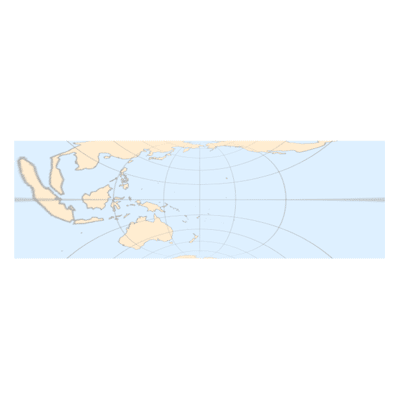
(正视图)
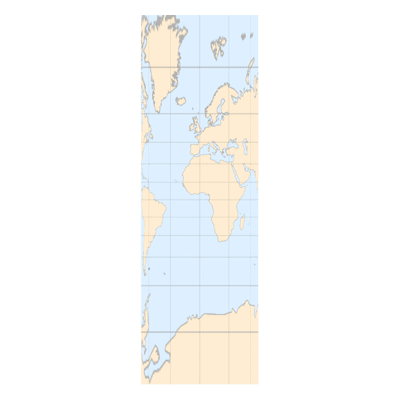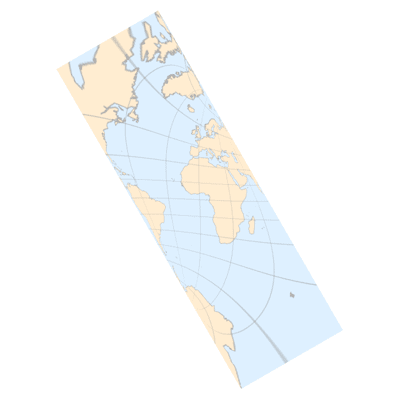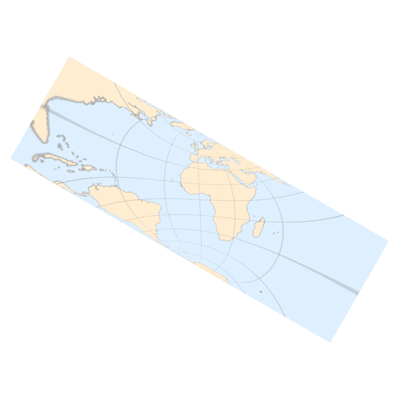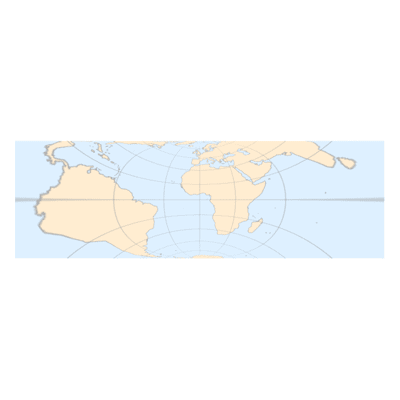
(后视图)

(俯视图)
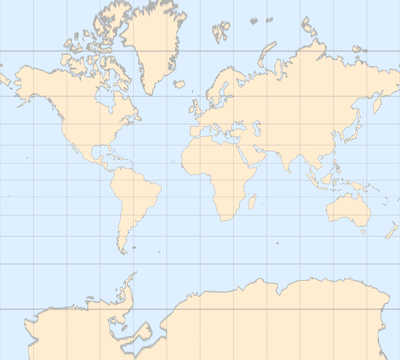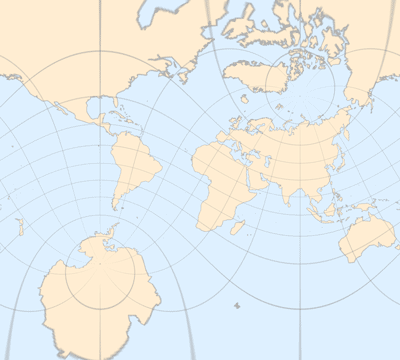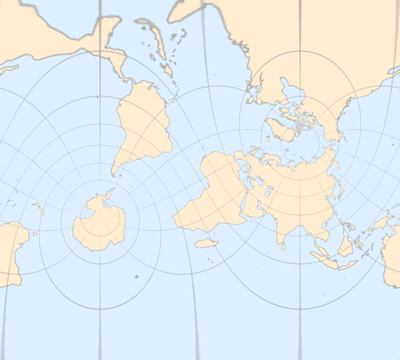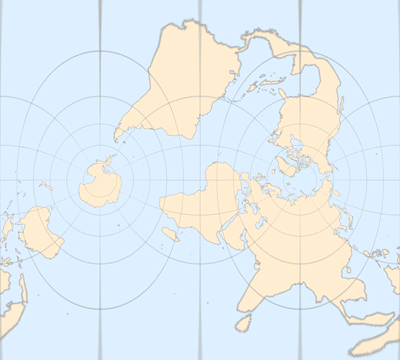
(平面图)

按照惯例,此处应该附上代码,但是这个代码写的并不优雅,渲染上面 4 张动图足足用了 1 小时 57 分钟,所以就不公开出来了。
关于 Mercator 投影的思考

(我并不是 GIS 专业的,这里斗胆谈一点个人的看法属于是,大佬勿嘲)
疑问
搜索 Mercator 投影,会常到见一种看似很有道理的言论:
假设地球被套在一个圆柱中,赤道与圆柱相切,然后在地球中心放一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,就形成以一幅墨卡托投影的世界地图。
很多人在科普 Mercator 投影时都会引用上面这句话,甚至某百科都是这么说的。为此,他们还做了一张示意图:
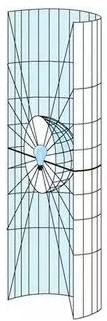
乍一听感觉道出了 Mercator 投影的本质,我一开始也深信不疑。但细细一品,果真如此的话,投影公式

从历史的角度来看,Mercator 投影是 1569 年提出的,此时微积分尚且没有发明,而且投影公式里的对数

所以,需要分清楚 Mercator 投影和 Mercator 的投影。1569 年,Mercator 出版了他的世界地图,他的确可能是根据“地球中心放一盏灯”这种说法绘制的地图。我们看下面这张邮票也体现着这种思想:

这是 Mercator 的投影。但是,Mercator 投影是后人修正后的。这多少有点类似明史与《明史》的关系。
探索
不妨尝试对比一下
纬度高于
把上面的邮票放大:

发现发光点并不在圆心,而是偏移了一定的距离???不妨假设地球半径是
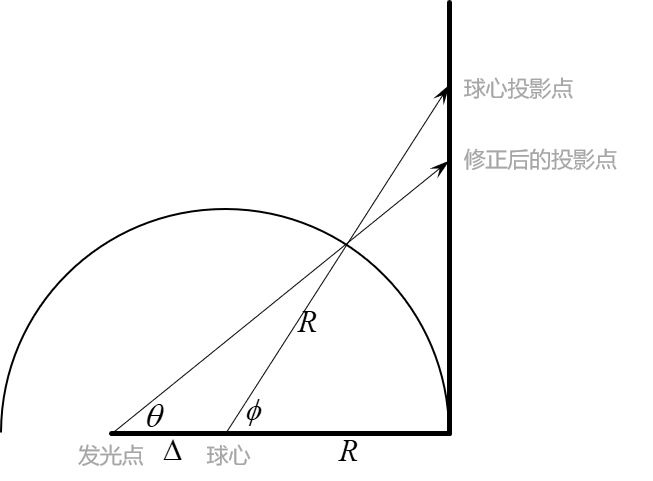
根据正弦定理:
反解出

那么,此时
这就是修正后的投影公式。如果令

尝试计算一下它的逆变换:

有点过于复杂。
那么这个
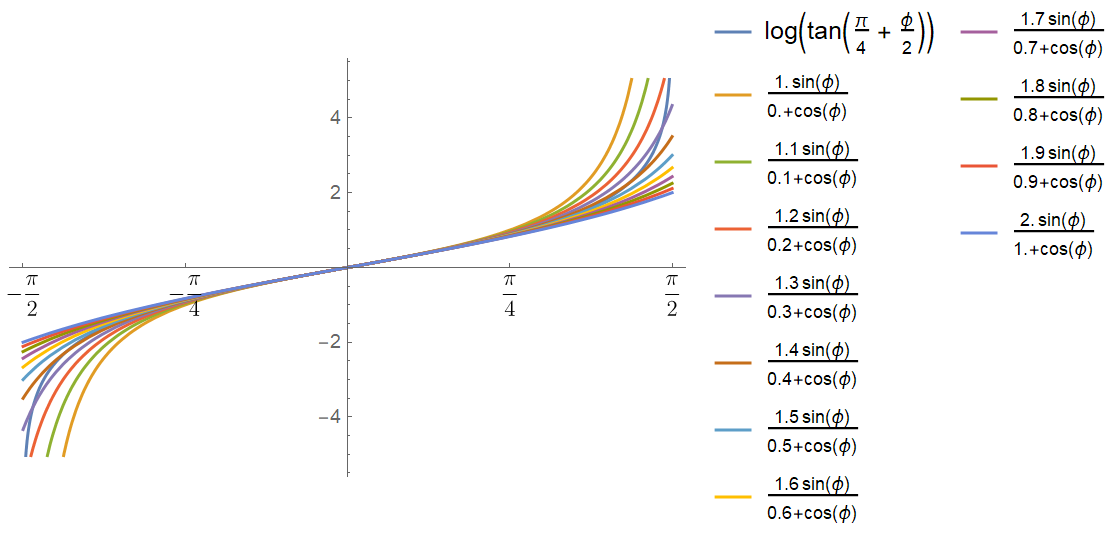
当

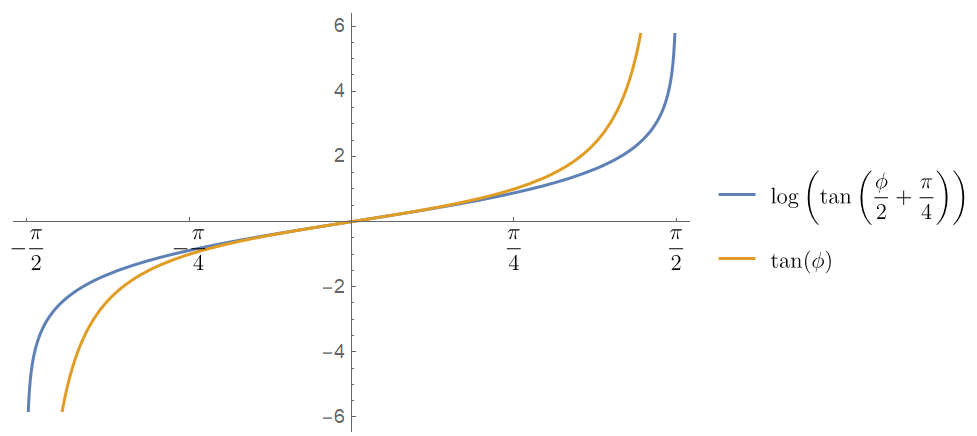
下面研究不同的发光点偏移与等角投影点的距离偏差,即下式的图像:
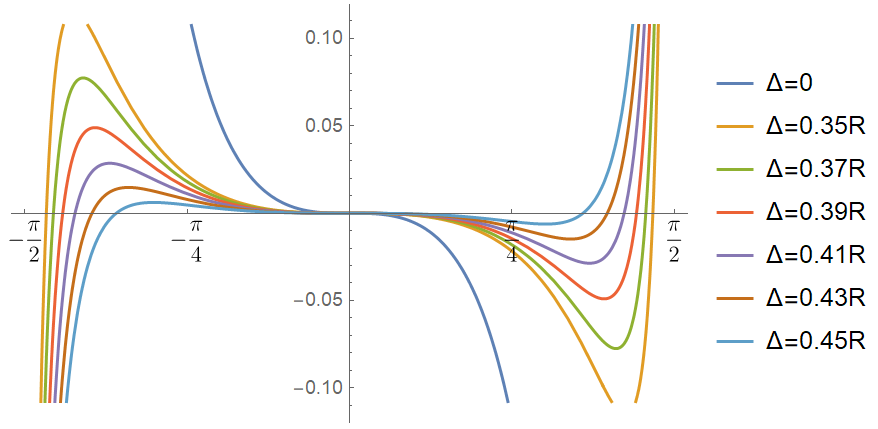
可以看出,在低于
结尾
强烈谴责Mathematica的中国地图不完整!!!
坚决抵制使用Mathematica绘制中国地图!!!
正确的中国地图如下:
Mercator 投影